Theoretische Haltekraft eines Sauggreifers
Zur Berechnung der theoretischen Haltekraft werden nachfolgend die drei wichtigsten und am häufigsten vorkommenden Lastfälle (Handhabungsabläufe) dargestellt und beschrieben.
Wichtig:
Bei den folgenden, vereinfachten Darstellungen der Lastfälle muss als Basis für die Berechnung der ungünstigste Lastfall mit der höchsten, theoretischen Haltekraft verwendet werden. Nur so kann sichergestellt werden, dass der Sauggreifer das Werkstück im gesamten Handhabungsvorgang sicher greift.
Sicherheitsfaktor S:
Je nach Beschaffenheit der Werkstückoberfläche muss der Sicherheitsfaktor S angepasst werden. Für den Sicherheitsfaktor wird ein Mindestwert von 1,5 für glatte und dichte Werkstücke angenommen. Bei kritischen inhomogenen, porösen, rauen oder geölten Werkstücken muss ein Sicherheitsfaktor von mindestens 2,0 oder höher angesetzt werden.
Reibwert μ:
Der Reibwert μ bezeichnet das Verhältnis von Reibungskraft zu Normalkraft. Allgemein gültige Angaben zum Reibwert zwischen Sauggreifer und Werkstück können nicht gemacht werden, daher muss der Reibwert μ durch Versuche konkret ermittelt werden.
Folgende Werte können als Richtwerte angesetzt werden.
| 0,2 ... 0,3 | für nasse Oberflächen |
| 0,5 | für Holz, Metall, Glas, Stein, ... |
| 0,6 | für raue Oberflächen |
Berechnung bei geölten Oberflächen:
Für Standardsauger bei denen in den technischen Daten keine Querkraft angegeben ist, wird als Richtwert μ = 0,1…0,3 empfohlen. Um einen genaueren Wert zu bekommen sind Tests mit dem Originalwerkstück durchzuführen.
Für Sauggreifer bei denen eine Querkraft auf trockener bzw. geölter Oberfläche explizit angegeben wird, kann der Reibwert μ nach folgender Formel bestimmt werden:
μ = FR / FN
Querkraft auf trockener bzw. geölter Oberfläche/Saugkraft
Der berechnete μ-Wert wird dann in die Formel des jeweiligen Lastfalls (I bis III) eingesetzt.
Typische Lastfälle
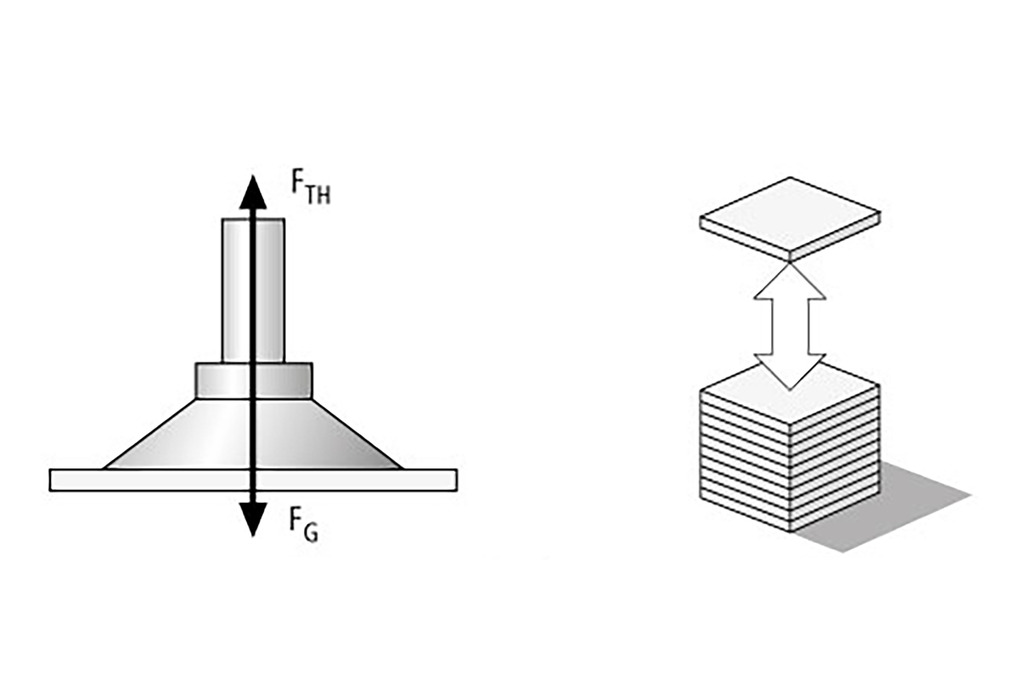
Lastfall I – Sauggreifer horizontal, Kraftrichtung vertikal
Das Werkstück (im vorliegenden Fall die Stahlplatte mit den Maßen 2,5 x 1,25 m) wird von einer Palette gehoben. Dabei wird das Werkstück mit einer Beschleunigung von 5 m⁄s² bewegt (keine Querbewegung).
FTH = m × (g + a) × S
FTH = theoretische Haltekraft [N]
m = Masse [kg]
g = Erdbeschleunigung [9,81 m/s2]
a = Beschleunigung [m/s2] der Anlage
S = Sicherheitsfaktor
Unser Beispiel:
FTH = 61,33 kg × (9,81 m/s2 + 5 m/s2) × 1,5
FTH = 1.363 N
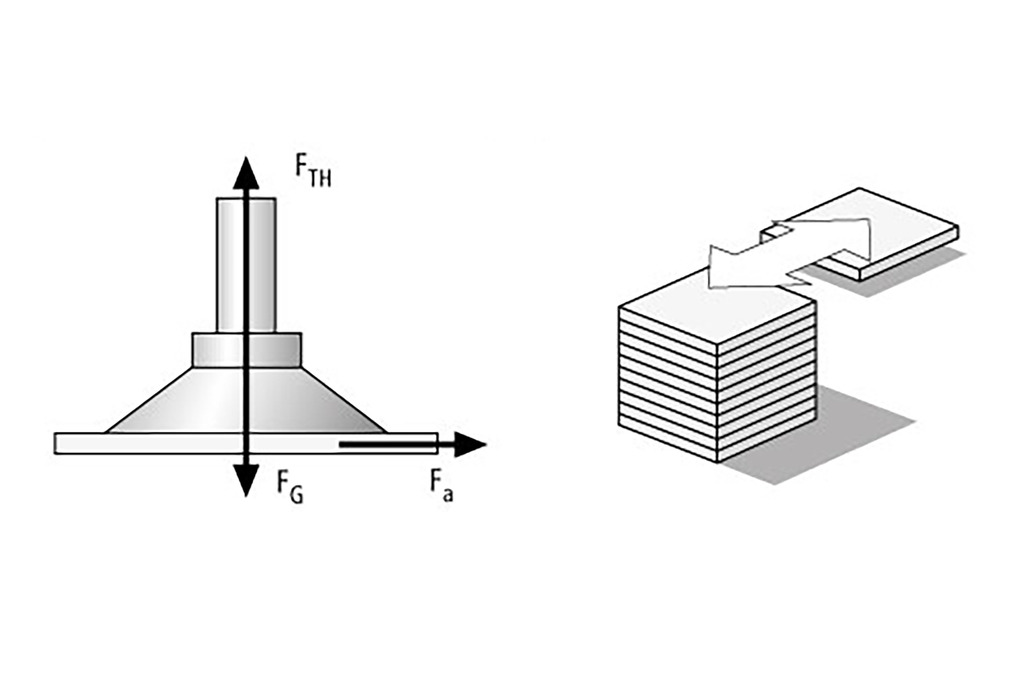
Lastfall II – Sauggreifer horizontal, Kraftrichtung horizontal
Das Werkstück (im vorliegenden Fall die Stahlplatte mit den Maßen 2,5 x 1,25 m) wird horizontal aufgenommen und horizontal transportiert. Die Beschleunigung liegt dabei bei 5 m/s².
FTH = m × (g + a ⁄ μ) × S
FTH = theoretische Haltekraft [N]
Fa = Beschleunigungskraft = m x a
m = Masse [kg]
g = Erdbeschleunigung [9,81 m/s2]
a = Beschleunigung [m/s2] der Anlage (Not-Aus-Situation beachten!)
μ = Reibwert
S = Sicherheitsfaktor
Unser Beispiel:
FTH = 61,33 kg × (9,81 m/s2 + 5 m/s2 ⁄ 0,5) x 1,5
FTH = 1.822 N
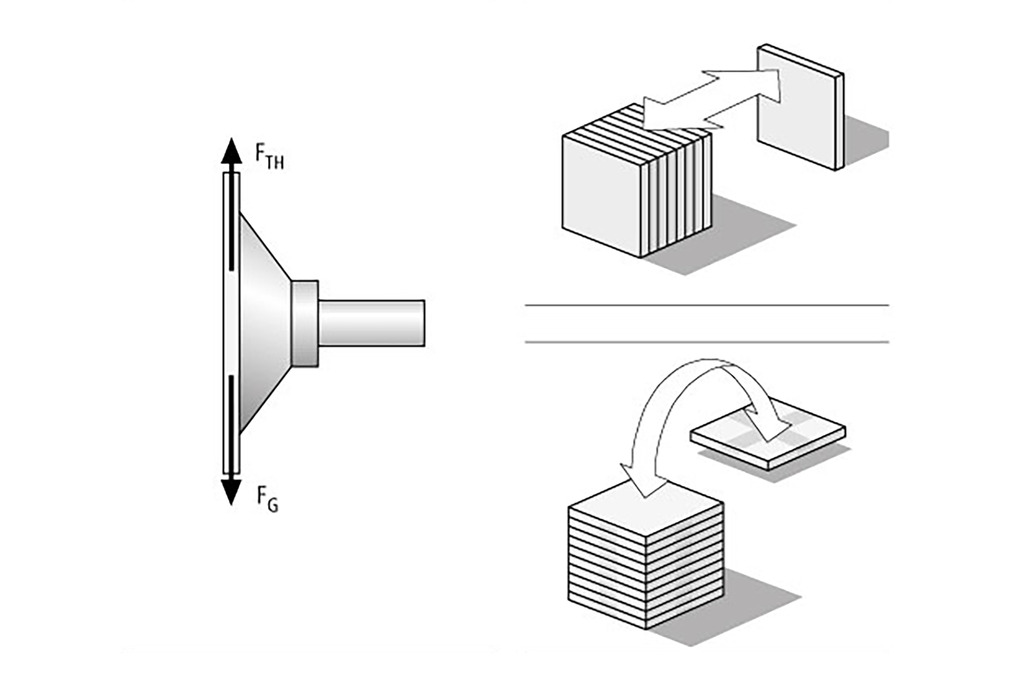
Lastfall III – Sauggreifer vertikal, Kraftrichtung vertikal
Beschreibung des Lastfalls: Das Werkstück (im vorliegenden Fall die Stahlplatte mit den Maßen 2,5 x 1,25 m) wird von einer Palette genommen und über eine Drehbewegung mit einer Beschleunigung von 5 m/s² umgesetzt.
FTH = (m ⁄ μ) × (g + a) × S
FTH = theoretische Haltekraft [N]
m = Masse [kg]
g = Erdbeschleunigung [9,81 m/s2]
a = Beschleunigung [m/s2] der Anlage
μ = Reibwert
S = Sicherheitsfaktor
Unser Beispiel:
FTH = (61,33 kg ⁄ 0,5) x (9,81 m/s2 + 5 m/s2) x 2
FTH = 3.633 N
Vergleich
Laut Aufgabenstellung wird das Werkstück von einer Palette gehoben, seitlich bewegt und auf einem Bearbeitungszentrum abgesetzt. Die Drehbewegung aus dem Lastfall III ist in der Anwendung nicht vorgesehen. Für das Beispiel muss daher lediglich das Ergebnis aus dem Lastfall II berücksichtigt werden. Damit ergibt sich für den vorliegenden Fall eine maximale theoretische Haltekraft (FTH) von 1.822 N. Diese theoretische Haltekraft wirkt auf den Sauggreifer beim horizontalen Transport des Werkstücks. Um die Aufgabenstellung sicher lösen zu können, basieren die folgenden Berechnungen auf diesem Wert.