Bir Vantuzun Teorik Tutma Kuvveti
Teorik tutma kuvvetini hesaplamak için, en önemli ve en sık meydana gelen üç yük durumunu (taşıma dizileri) gösterip açıklıyoruz.
Önemli:
Aşağıdaki yük durumlarının basitleştirilmiş gösterimleri için hesaplama, en yüksek teorik tutma kuvvetine sahip en kötü yük durumuna göre yapılmalıdır. Bu, vantuzun tüm taşıma süreci boyunca iş parçasını güvenli bir şekilde kavramasını sağlamanın tek yoludur.
Güvenlik faktörü S:
Güvenlik faktörü S, iş parçası yüzeyinin durumuna göre ayarlanmalıdır. Güvenlik faktörü, pürüzsüz ve yoğun iş parçaları için minimum 1,5 değerine sahiptir. Kritik, heterojen, gözenekli, pürüzlü veya yağlı iş parçaları için 2,0 veya daha büyük bir güvenlik faktörü kullanılmalıdır.
Sürtünme katsayısı μ:
Sürtünme katsayısı μ, sürtünme kuvveti ile normal kuvvet arasındaki ilişkiyi tanımlar. Vantuz ve iş parçası arasındaki sürtünme katsayısı için genel olarak geçerli spesifikasyonlar yayınlayamıyoruz. Sürtünme katsayısı μ bu nedenle testler yoluyla doğru bir şekilde belirlenmelidir.
Referans değerler olarak aşağıdakiler kullanılabilir.
| 0.2 ... 0.3 | ıslak yüzeyler için |
| 0.5 | ahşap, metal, cam, taş vb. için |
| 0.6 | pürüzlü yüzeyler için |
Yağlı yüzeyler için hesaplama:
Belirlenmiş yanal kuvveti olmayan standart vantuzlar için önerilen referans değeri μ = 0,1 ila 0,3'tür. Daha kesin bir değer elde etmek için, testler orijinal iş parçası üzerinde tamamlanmalıdır.
Kuru veya yağlı bir yüzey üzerinde açıkça belirtilen bir yanal kuvvete sahip vantuzlar için, sürtünme katsayısı μ aşağıdaki formül kullanılarak hesaplanabilir:
μ =FR / FN
Kuru veya yağlı bir yüzey üzerindeki yanal kuvvet/emme kuvveti
Hesaplanan μ değeri daha sonra ilgili yük durumunun (I ila III) formülünde kullanılabilir.
Tipik yük durumları
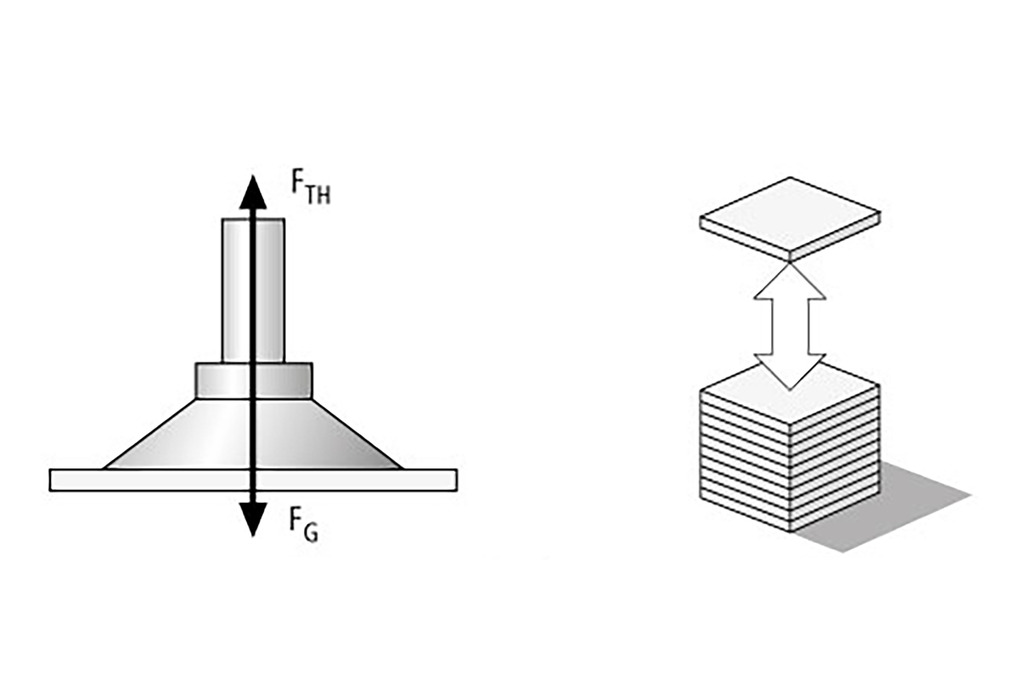
Yük durumu I - Vantuz yatay, kuvvet yönü dikey
İş parçası (bu durumda 2,5 x 1,25 m boyutlarında çelik sac) bir paletten kaldırılır. İş parçası 5 m/s2 'lik bir ivme ile kaldırılır (enine hareket yok).
FTH = m × (g + a) × S
FTH = teorik tutma kuvveti [N]
m = Ağırlık [kg]
g = Yerçekimi [9,81 m/s2]
a = Sistemin ivmesi [m/s2]
S = Güvenlik faktörü
Bizim örneğimiz:
FTH = 61,33 kg × (9,81 m/s² + 5 m/s²) × 1,5
FTH = 1.363 N
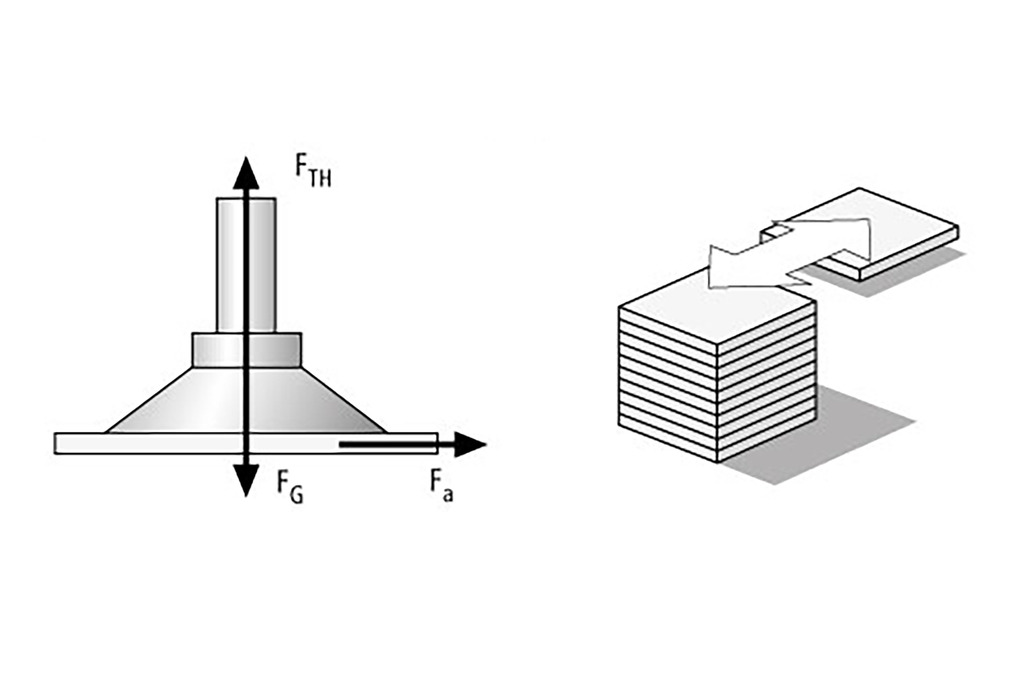
Yük durumu II - Vantuz yatay, kuvvet yönü yatay
İş parçası (bu durumda 2,5 x 1,25 m boyutlarında çelik sac) dikey olarak yukarı kaldırılır ve yatay olarak taşınır. İvme 5 m/s²'dir.
FTH = m × (g + a ⁄ μ) × S
FTH = teorik tutma kuvveti [N]
Fa = İvme kuvveti = m x a
m = Ağırlık [kg]
g = Yerçekimi [9,81 m/s2]
a = Sistemin ivmesi [m/s2] (Acil Durdurma durumlarını aklınızda bulundurun!)
μ = Sürtünme katsayısı
S = Güvenlik
Bizim örneğimiz:
FTH = 61.33 kg × (9.81 m/s2 + 5 m/s2 ⁄ 0.5) x 1.5
FTH = 1,822 N
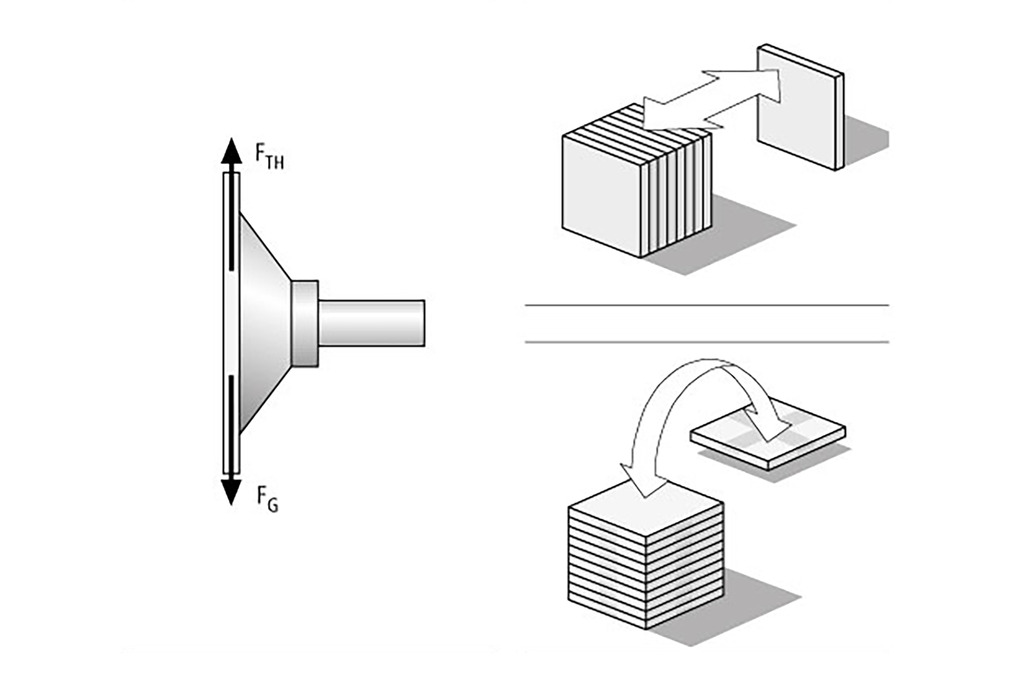
Yük durumu III - Vantuz dikey, kuvvet yönü dikey
Yük durumunun açıklaması: İş parçası (bu durumda 2,5 x 1,25 m boyutlarında çelik sac) bir paletten alınır ve 5 m/s2'lik bir ivmeyle dönme hareketiyle hareket ettirilir.
FTH = (m ⁄ μ) × (g + a) × S
FTH = teorik tutma kuvveti [N]
m = Ağırlık [kg]
g = Yerçekimi [9,81m/s2]
a = Tesisin ivmesi [m/s2] (Acil Durdurma durumlarını aklınızda bulundurun!)
μ = Sürtünme katsayısı
S = Güvenlik
Bizim örneğimiz:
FTH = (61.33 kg ⁄ 0.5) x (9.81 m/s2 + 5 m/s2) x 2
FTH = 3,633 N
Karşılaştırma
Senaryomuzda, iş parçası bir paletten kaldırılır, yana doğru hareket ettirilir ve bir işleme merkezine yerleştirilir. Bu uygulamada yük durumu III'teki dönme hareketine gerek yoktur, bu nedenle yalnızca yük durumu II'den elde edilen sonucun dikkate alınması gerekir. Bu durumda elde edilen sonuç 1.822 N'luk maksimum teorik tutma kuvvetidir (FTH). Bu teorik tutma kuvveti, iş parçasının yatay taşınması sırasında vantuza etki eder. Aşağıdaki hesaplamalar, görevi güvenli bir şekilde çözmek için bu değere dayanmaktadır.